Answer (1 of 3) \left { \quad \dfrac { 1 2 \sin ^ { 2 } x } { 1 \sin 2 x } } \\ { =\dfrac { \cos ^ { 2 } x \sin ^ { 2 } x 2 \sin ^ { 2 } x } { \cos ^ { 2⇔2tan 2 x−2tanx−3=0 ⇔tanx=1±√7/2 Các giá trị này thỏa mãn điều kiện nên là nghiệm của phương trình b) cos 2 x=3sin2x3 Ta thấy cosx = 0 không thỏa mãn phương trình Với cosx ≠ 0, chia hai vế của phương trình cho cos 2 x ta được 1=6tanx3(1tan 2 x) ⇔3tan 2So the popular practice is to write tan2x when we

1 Cos 4 X Sinº X Cos 2x 6 6 2 Sin X Cos X Homeworklib
2tanx/1+tan^2x=2sinxcosx
2tanx/1+tan^2x=2sinxcosx-Like, I know you can keep splitting the angle in terms of sums of x and 2x if it is tan3x, or 3x and 2x and then the respective formulas in tan5x, so on and so forth, but is there any way to get a general formula, like tan2x= 2tanx/(1tan 2(x)), etcSin(2x) = 2sinxcosx cos(2x) = cos2 x sin2 x tan(2x) = sin(2x) cos(2x) Note These formulas are derived from the sum formulas in 54 using 2x= xx The formula for cos2xcan also be written as cos(2x) = cos2 x sin2 x = 2cos2 x 1 = 1 2sin2 x The formula for tan(2x) can be written as tan(2x) = 2tanx 1 tan2 x Example 1 Solve the following equations



How To Show That 2sinx Cosx 4cos X 1 May Be Written In The Form Tan X 2tanx 3 0 Quora
Prove the identities 1 2cos2x(22tan^2x)/(1tan^2x) 2 2sinxcosx(22cos^2x)/tanx 3 2sin^2x22cos^2x 4 2sin2x4tanxcos^2x 5 (4tanx)/(tan2x)22tan^2xDoubleAngle identities are formulas expressing trigonometric functions of an angle 2x in terms of functions of an angle x, sin(2x) = 2sinxcosx cos(2x) = cos^2xsin^2x = 2cos^2x1 = 12sin^2x tan(2x) = (2tanx)/(1tan^2x)Let's prove!!sin 2x= 2 sin x cos x LHS sin2x sin (x x)=sinx cosx cosx sinx = 2 sinX cosX LHS = RHSlET'S PROVE!cos 2XOur guarantees Delivering a highquality product at a reasonable price is not enough anymore That's why we have developed 5 beneficial guarantees that will make your experience with our service enjoyable, easy, and safe
tan x = sin x cos x \displaystyle \tan { {x}}=\frac { { \sin { {x}}}} { { \cos { {x}}}} tanx = cosxsinx X Just remember `tanx = (sinx)/ (cosx)` Re Trig identity (sinxcosx)^2tanx = tanx2sin^2x Alexandra , 0544 ( 1 2 sin x cos x) tan xCos^2X=?—— sin2x= 2sinx*cosxcos2x=cos^2x sin^2x = 2cos^2x 1 = 1 2sin^2x另外有一个万能公式cos2x= ( 1 tan^2x)/ (1tan^2x)sin2x= 2tanx / (1tan^2x) sin^2X的导是多少—— y=sin²x y′=2sinxcosx =sin2x 高一数学求解1 2sin^2X等于多少1tanxtany Double angles sin(2x) = 2sinxcosx cos(2x) = cos2 x sin2 x = 2cos2 x 1 = 1 2sin2 x tan(2x) = 2tanx 1 tan2 x 2 Half angles sin x 2 = r 1 cosx 2 cos x 2 = r 1cosx 2 tan x 2 = 1 cosx sinx = sinx 1cosx Power reducing formulas sin2 x= 1 cos2x 2 cos2 x= 1cos2x 2 tan2 x= 1 cos2x 1cos2x Product to sum
Answer Expert Verified this is true for all real value of x then , sin2x = 2sinx What is 2tanx equal to?化简1/(1 tanx) 1/(1tanx) 的详解 化简先通分1/(1tanx)1/(1tanx)=(1tanx)(1tanx)/(1tanx)(1tanx)=2tanx/(1tan²x)=2tanx/(1sin²x/cos²xPurplemath In mathematics, an "identity" is an equation which is always true These can be "trivially" true, like "x = x" or usefully true, such as the Pythagorean Theorem's "a 2 b 2 = c 2" for right trianglesThere are loads of trigonometric identities, but the following are the ones you're most likely to see and use
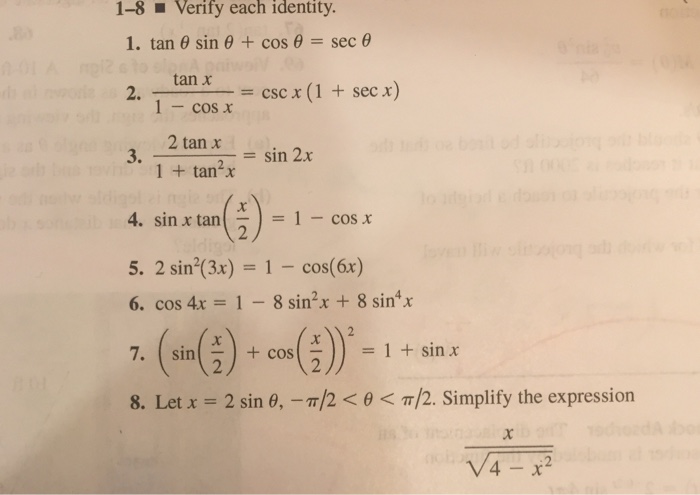



2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula




Pembuktian Trigonometri Fahmi Harits S Personal Blog
656am #2 Jhun Vert $\sin 2x = 2 \sin x \cos x$ $= \dfrac{2 \sin x \cos x}{\cos x \sec^2 x} \cdot \cos x \sec^2 x$ The equation says, sin2x=2sinxcosx =2tanx/1tan^2x How did they get 2tanx/1tan^2x?It can not be proved because 2 tan x sin 2x/2sin²x =2 tan x 2sinx cosx/2sin²x = 2 tan x cos x/sin x = 2 tan x cot x = 2tan x 1/tan x which can't be equal to tan x for any value of x




Math22 1reviewerderivativetrigonometricfunction Pdf Trigonometric Functions Mechanics
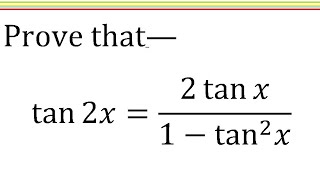



Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube
化简1/(1 tanx) 1/(1tanx) 的详解—— 化简先通分1/(1tanx)1/(1tanx)=(1tanx)(1tanx)/(1tanx)(1tanx)=2tanx/(1tan²x)=2tanx/(1sin²x/cos²x 1 CÁC CÔNG THỨC LƯỢNG GIÁC CƠ BẢN Biên soạn và thực hiện vi tính NguyÔn §øc B¸ GV THPT TIỂU LA THĂNG BÌNH I/Các hệ thức cơ bản sin 2 x cos 2 x cosx sinx π , (x ≠ kπ) , (x ≠ kπ) c otx= cosx 2 sinx 1 π 1 = 1 tan 2 x, (x ≠ kπ) 2 = 1 cot 2 x, (x ≠ kπ) 2 sin x cos 2 x t anx= =1 t anxAnswer (1 of 4) (tan x1)^2=(12sin xcos x)/(cos^2 x) LHS =(tan x1)^2 =(sin x/cos x1)^2 ={(sin xcos x)/cos x}^2 =(sin x cos x)^2 /(cos^2 x) =(sin^2 x cos^2x 2sin xcos x)/(cos^2 x) =(12sin xcos x)/(cos^2 x)




Solved 55 Show That The Equation A 2sin X 4 Cos X 1 Chegg Com



What Is The Formula Of Tan2x Quora
Use the sum and difference identities 14 cofunctionThe value of cos2x will be between −1 and 1 Does sin 2x 2sinxcosx?Power reducing Identity tan^2 x 1 cos (2x) / 1 cos (2x) half angle formula for sine sin (x/2) = / square root of ( 1cosx ) / 2 half angle formula for cosine cos (x/2) = / square root of ( 1 cosx ) / 2 half angle formula for tangent tan (x/2) = ( 1cosx ) / (sinx)




3 If Sin X Cos X 1 5 Then Tan 2x Is Equal To A 25 17 B 25 7 D 7 25 14 General Solution Of The Equation C 24 7




Prove That Tan2x 2tanx 1 Tan X Brainly In
Homework Statement cosx=12/13 3pi/2 is less than or equal to x is less than or equal to 2pi Homework Equations sin2x = 2sinxcosx cos2x = 12(sinx)^2 tan2x = (2tanx)/(1(tanx)^2) The Attempt at a Solution Using the tan2x formula, I getStarting with the left hand side, the first thing to change is the sin2x, because the expression on the RHS only has terms of x, not 2xUsing the identity sin2x = 2sinxcosx, the expression becomes 2sinxcosx/ (1 (tan 2 x))Next, we will change the tan 2 x to (sinx/cosx) 2 This will give a fraction on the demoninator, which we will want to get rid of, so the next step is to multiply top andSin2x Is Tan 2x and TANX 2 the same?




Prove That Sin2x 2tanx 1 Tan X Youtube




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula
S Sin cos tan csc sec cot Rate 0 No votes yet Top 795 reads; Prove that sin2x = {(2sinxcosx), (2tanx/(1 tan2x)) We have sin(x y) = sin xcosy cosxsiny Replacing y by x we get sin 2x = 2sinx cosx Which doubleangle or halfangle identity would you use to verify the followingcscxsecx=2csc2x a) cos2x=1sin^2x b)sin2x=2sinxcosx c)tan2x= (2tanx)/ (1tan^2x) d)cos2x=2cos^2x1 2 See answers report flag outlined bell outlined




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula




1 Cngthclnggic Sinx Tanx Cotx 1 1 2 1 3 Cngthcnhn Oelig I Sin2x 2sinxcosx Tan2x 2tanx 1 2tan
SOLUTION Find sin (2x), cos (2x), and tan (2x) from the given information sec (x) = 10 x in quadrant 42sinxcosx cos2x cos^2xsin^2x tan2x 2tanx/1tan^2x sin a/2 √1cosA/2 cos a/2 √1cosA/2 tan a/2 1cosA/sinA Other sets by this creator Biology exam 1 31 terms Maddy_bowers13 exam 4 terms 71 terms Maddy_bowers13 Joints 33 terms Maddy_bowers131 tan 2 x = sec 2 x 3 cotangent version of pythagorean identity 1 cot 2 x = csc 2 x 4 (2x) = 2sinxcosx 11 double angle identity for cosine cos2x = cos 2 x sin 2 x double angle identity for tangent tan2x = (2tanx) / (1 tan 2 x) 13 how do you prove cofunction identities?




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula




If X 30 Verify That I Tan2x 2tanx 1 Tan 2x Ii Sinx Sqrt 1 Cos2x 2 Youtube
I need to prove that the following is true Thanks (2tanx /1tan^x)(1/2cos^2x1)= (cosxsinx)/(cosx sinx) and thanks check your typing I tried 30º, the two sides are not equal, they differ by 1 oh , thank you Mr Calculus Integrate 1/sinx dx using the identity sinx=2(sin(x/2)cos(x/2)) a sin x cos x = 1 2sin 2x b tanx 3cot3x = 2tanx c tanx cot2x = 8cos 2 x d1 sinxcosx(2sin2x cos 2 2x) = 0 etan 2 xtan 3 x = 1 f tan(x pi/12)cot(pi/4 x) = 2 căn3Sin 2xcos x= 1 1tan2 x= sec2 x 2 SumDifference formulas sin(x y) = sinxcosy sinycosx cos(x y) = cosxcosy sinxsiny tan(x y) = tanx tany 1 tanxtany cot(x y) = cotxcoty 1 cotx coty arctan( ) arctan( ) = arctan 1 3 Double Angle formulas sin2x= 2sinxcosx cos2x= cos 2x sin2 x= 2cos x 1 = 1 2sin2 x tan2x= 2tanx 1 2tan x 4 Half Angle formulas sin



2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube
Hey guys,I need some help on the following trig identities 1) sin2x = 2tanx/1tan^2x 2) sin2x/sinx cos2x/cosx = secx My attempts 1) LS sin2x 2sinxcosx 2sinx/cosx 2tanx/1tanx Not sure if this is right or not I kind of understand my third step but it just doesn't seem Thanks (2tanx /1tan^x)(1/2cos^2x1)= (cosxsinx)/(cosx sinx) and thanks Trigonometric Identities Prove (tanx secx 1)/(tanx secx 1)= tanx secx My work 3=0 now you have a quadratic, solve for cos x using the equation cosx=( 5Sin (b) Cos (a)Cos (b) Therefore, sin (xx) = sin (x)cos (x) cos (x)sin (x) = 2 sin (x) cos (x) Also, Sin 2x = 2 t a n x 1 tan 2 x To Prove Sin2x in the form of tanx x which is equal to 2 t a n x 1 tan 2 x Now let us start the proof from the righthand side and hence, prove it as LHS = RHS
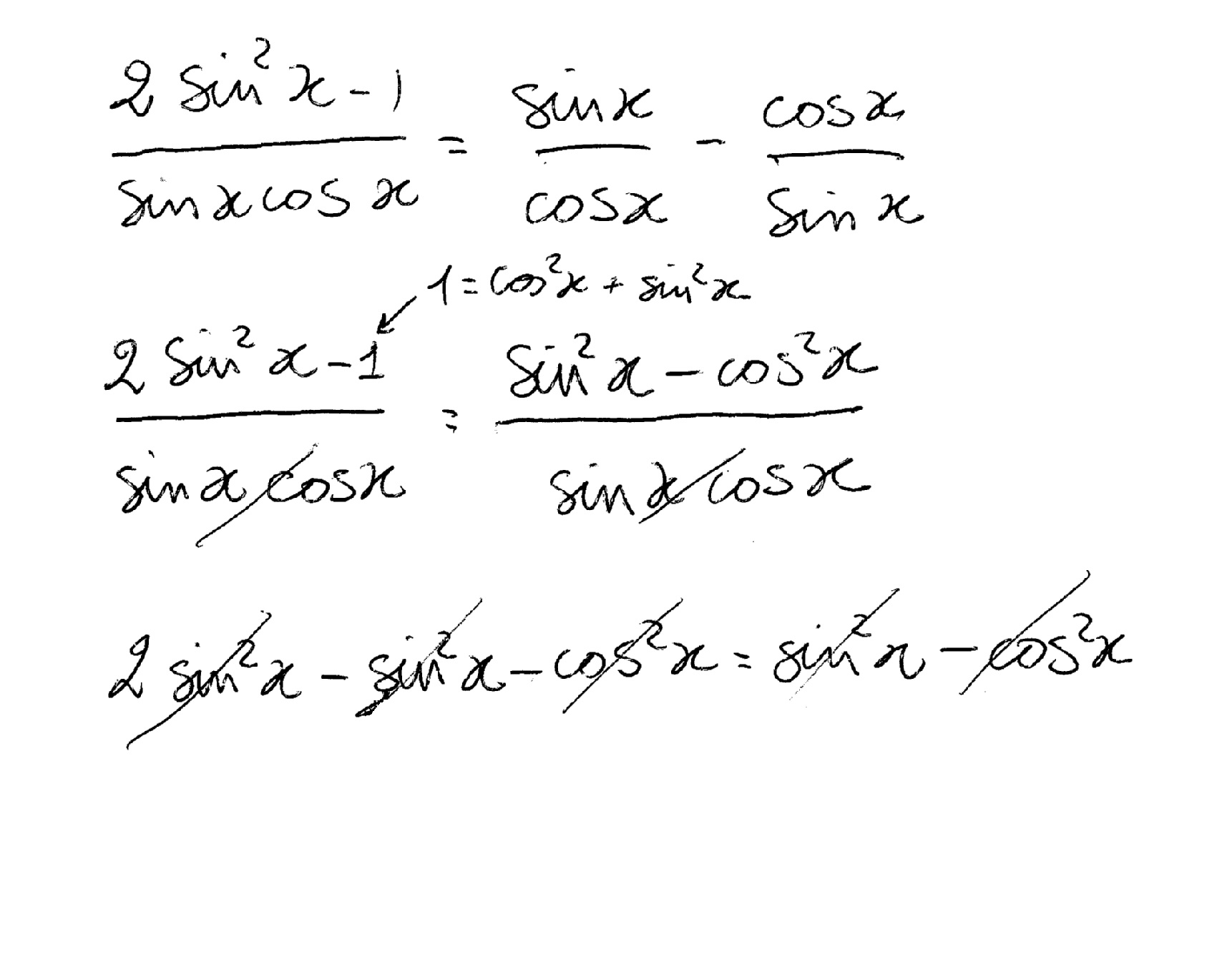



How Do You Prove 2sin 2x 1 Sinxcosx Tanx Cotx Socratic




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube
Sin(2x) = 2sinxcosx Cos(2x) = Cosˆ2x – Sinˆ2x = 2cosˆ2x 1 = 1 2sinˆx 1 Tan(2x) = 2tanx/1tanˆ2x If you are looking for Trig Hyperbolic Identities for Trig Double Angle identities then here comes You can also learn about Hyperbolic Trig Identities—— 2cos (x)^2 再看看别人怎么说的 sin^2X=? Please see below (2tanx)/(1tan^2x) = (2sinx/cosx)/sec^2x = (2sinx/cosx)/(1/cos^2x) = (2sinx)/cosx xx cos^2x/1 = 2sinxcosx = sin2x




Prove Tan2x 2tanx 1 Tan 2 X Maths Introduction To Trigonometry Meritnation Com
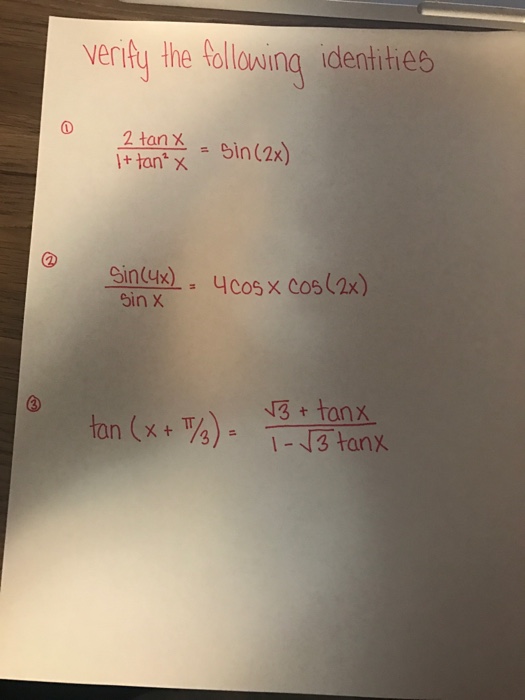



2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula
Toán 10 BT Lượng giác Các bạn giúp, mai em thi lại rồi (Thảo luận trong 'Thảo luận chung' bắt đầu bởi huydaigia22, Tháng năm 12Yes, if the term at the bottom is tan^2 x, you typed tan^x, and I read it as tan x I got the proof, give me a bit of time to type it I'm sorry Mr Reiny you are right it is tan^2x LS= 2tanx/ (1tan^2x) 1/ (2cos^2x 1) = 2sinx/cosx 1/ (1sin^2x/cos^2x) 1/ (2cos^2x (sin^2x cos^2x))Sin (2x) = (2tan (x)) / (1tan^2 (x)) *** Start with RHS 2tanx/ (1tan^2x) 2tanx/ (sec^2x) 2 (sinx/cosx)/ (1/cos^2x) 2sinxcosx=sin2x verifiedRHS=LHS




Prove That Sin2x 2tanx 1 Tan X Youtube



2
4 Chapter 10 Techniques of Integration EXAMPLE 1012 Evaluate Z sin6 xdx Use sin2 x = (1 − cos(2x))/2 to rewrite the function Z sin6 xdx = Z (sin2 x)3 dx = Z (1− cos2x)3 8 dx = 1 8 Z 1−3cos2x3cos2 2x− cos3 2xdx Now we have four integrals to evaluate Z 1dx = x and ZProve as an identity;2sinxcosx cos2 x sin2 x 2sinxcosx 1 = 2sinxcosx = sin(2x) = LHS bb cos(2x) = 1 1 tan(2x)tanx Ans RHS = 1 1 tan(2x)tanx = 1 1 2tanx 1 tan2 x tanx = 1 1 2tan2 x 1 2tan x = 1 1 tan2 x 1 tan2 x 2tan2 x 1 tan2 x 1




Analytic Trig Ppt Video Online Download




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic
Log in or register to post comments;




Misc 10 Sin X 1 4 Find Sin X 2 Cos X 2 Tan X 2




3 Trigonometric Equation And Identities
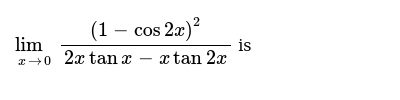



Which Double Angle Or Half Angle Identity Would You Use To Verify



2




Tan2x ただの悪魔の画像



What Is The Formula Of Tan2x Quora



Tan2x ただの悪魔の画像




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula




5 1 Using Fundamental Identities Ogden Gov




Tinkutara Equation Editor Math Forum Question



1



Sin 2x 1 Cos 2x 2 Csc 2x Tan X




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula
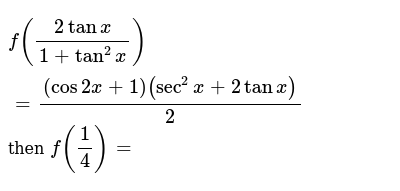



F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2 Then F 1 4



2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula




Solved Mixed Exercises For Exercises 69 72 Factor The Chegg Com




Chapter 7 Trigonometric Identities And Equations Ppt Download



1



How To Show That 2sinx Cosx 4cos X 1 May Be Written In The Form Tan X 2tanx 3 0 Quora




Tinkutara Equation Editor Math Forum Question




7 4 Proving Trigonometric Identities In This Unit We Ll Be Using Some Formula S That Are Also Found And Used In Unit 7 2 And 7 3 Here We Ll Be Solving Problems To Show That Both Sides Of The Equation Equal Each Other These Formulas Will Help Solve Some Trig




Warm Up Evaluate Each Expression Without Using A Calculator 1 Sin285 2 Cos285 3 Sin Ppt Download




Solved Section 5 3 Exercises Skills 2 If Sinx And Cosx 0 Chegg Com




1 Cngthclnggic Sinx Tanx Cotx 1 1 2 1 3 Cngthcnhn Oelig I Sin2x 2sinxcosx Tan2x 2tanx 1 2tan



2




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula



Cos2x Cos2x Has Quite A Few Formulas 1



Lcps Org




គណ តវ ទ យ ថ ន ក ទ ១១ កម រ តម លដ ឋ ន Pages 101 150 Flip Pdf Download Fliphtml5



How To Show That 2sinx Cosx 4cos X 1 May Be Written In The Form Tan X 2tanx 3 0 Quora




Tan2x ただの悪魔の画像



2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula



Bestpixtajpgjgh If F 2tanx 1 Tan 2x 1 Cos2x Sec 2x 2tanx 2 Then F 4




Proof For Tan 2x 2tanx 1 Tan X Trigonometry Youtube



2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula



2



Prove Sin2x 2tanx 1 Tan 2x Socratic




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube
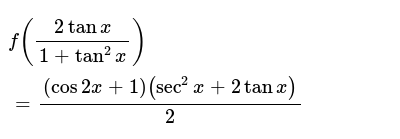



F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2




Integral Calculus



2



What Is The Result Of Tanx If 1 Cosx 1 Sinx 2 Quora




Warm Up Evaluate Each Expression Without Using A Calculator 1 Sin285 2 Cos285 3 Sin Ppt Download



Msaudia Weebly Com




Tinkutara Equation Editor Math Forum Question




Old Version Trig Show Sin 2x 2 Sin X Cos X 2tan X 1 Tan 2 X Youtube
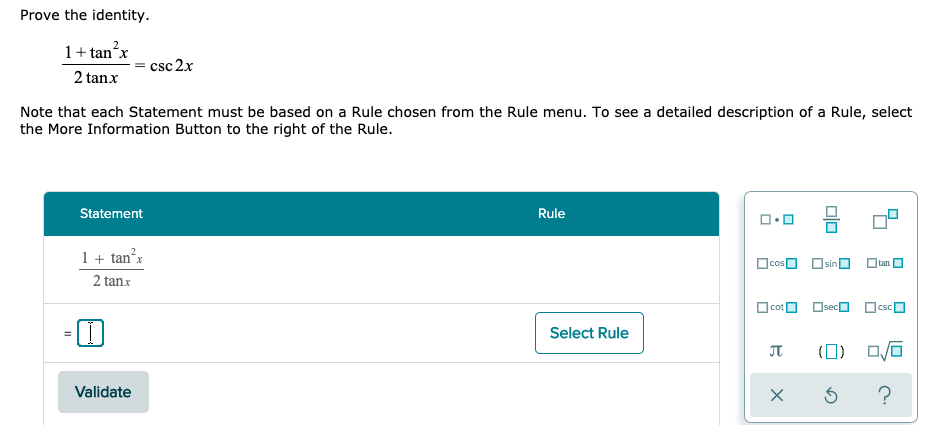



2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula




Chapter 7 Trigonometric Identities And Equations Ppt Download




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula



Tinkutara Equation Editor Math Forum Question




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula




Mathematics For Life Posts Facebook




By Siby Sebastian Pgt Maths Ppt Download




Which Of The Following Are Identities Check All That Apply A 1 Tan 2 X 2tan X 1 Tan2x B Brainly Com




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula



2tanx



Is Tanx 2 2tanx 1 5tanx Sec X Quora




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula
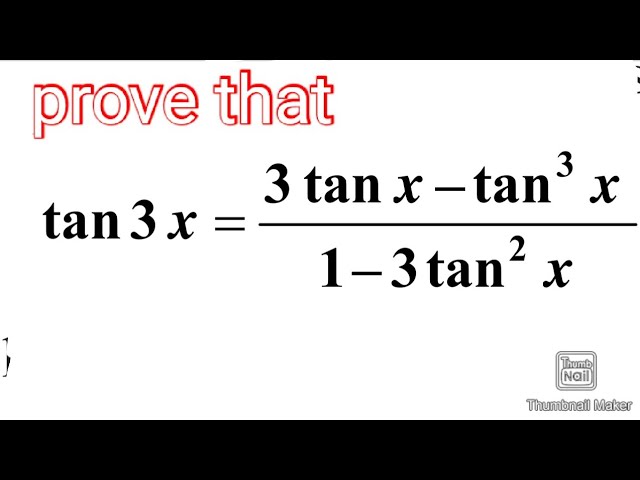



Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube



If Tanx 12 13 Evaluate 2 Sinx Cosx Cos 2x Sin 2x




Solutions To Homework Problems From Section 7 3 Of Stewart 1



2




Yoyoma Prelude To Math Www Youtube Comwatch




Solved Mixed Exercises For Exercises 69 72 Factor The Chegg Com




Misc 10 Sin X 1 4 Find Sin X 2 Cos X 2 Tan X 2 Chapter 3
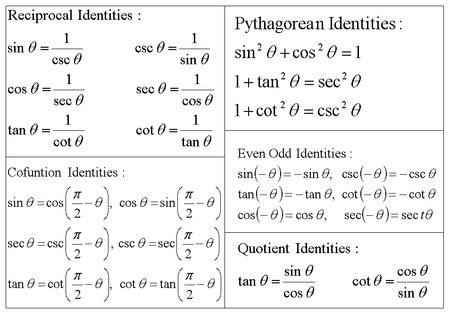



Proving Identities Trigonometry Socratic




Chapter 9 Notes



Cbsd Org



How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora




1 Cos 4 X Sinº X Cos 2x 6 6 2 Sin X Cos X Homeworklib



Cbsd Org




Trig Double Identities Trigonometric Double Angle Functions Trig




Solved 55 Show That The Equation A 2sin X 4 Cos X 1 Chegg Com



2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula



Tan2x ただの悪魔の画像



1




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula
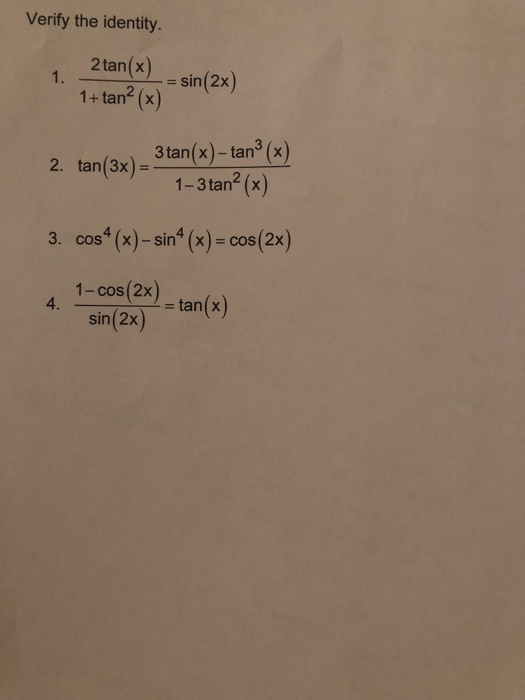



Solved Verify The Identity 2tan X Sin 2x 1 Tan2 X 2 Chegg Com



0 件のコメント:
コメントを投稿